自1883年雷诺的管流实验起,线性稳定的粘性剪切层流向湍流的转变或亚临界转捩机制一直是流体力学、物理学和应用数学领域的公开问题。亚临界转捩过程的主要特征之一是存在局地的湍流结构,如管流中的湍塞和槽流中的湍流带。由于这类结构的多尺度特性和强非线性,迄今为止,人们仍未能依据流体运动方程(Navier-Stokes方程)从理论上判断其自维持性,也无法理论求得亚临界转捩的源起或阈值雷诺数。
压差驱动的二维槽流是管流和三维槽流的简化模型,其亚临界转捩特征结构是局地的波包。陶建军课题组针对二维槽流,通过非线性非模态优化方法求得了导致亚临界转捩的最优扰动,给出了从最优扰动演化为局地波包的三个阶段及相应的控制机制。进一步地,通过提出保形近似并基于流动的扰动动能方程,给出了转捩的阈值雷诺数以及转捩结构扰动动能的表达式,理论预测同数值模拟结果相符。

图1. 二维槽流中最优扰动演化为转捩特征结构局地波包的第一、二阶段。 u和v分别为流向和法向扰动速度。雷诺数Re=3000,(t1, t2, t3, t4, t5)=(8.90, 13.55, 17.16, 22.89, 37.78)。[1]
不同强度和形式的扰动可在不同的雷诺数诱发转捩,这些雷诺数的最小值即为转捩的阈值雷诺数,即在低于该雷诺数时任何扰动均无法诱发转捩,它标志着转捩的源起阶段。对于由超临界不稳定性引导的转捩,其最优扰动(能诱发转捩的扰动动能最小的扰动)是线性不稳定模态。但对于亚临界转捩,必须考虑非线性作用的影响。对于二维槽流,之前人们认为局地波包是通过有限幅值TS波的亚谐不稳定性产生的。然而近期的研究表明,在雷诺数低于2600时不存在有限幅值的TS波但仍可激发出局地波包,这是亚谐不稳定性机制无法解释的。课题组通过非线性非模态优化方法,发现二维槽流最优扰动是往上游倾斜的波包(见图1,t=0),其演化为转捩特征结构(局地波包)的过程可分为三个阶段。在第一阶段,初始扰动在Orr机制作用下向下游偏转(图1中t=0至t3)并经历扰动动能的瞬态增长;在第二阶段,短波贡献的雷诺应力产生大尺度涡结构并在背景剪切作用下导致波包上下游结构的非对称性,即发生对称破缺,形态逐步接近局地波包不稳定的下支解(图1中t=t4至t=200);在第三阶段,扰动形态基本保持不变,但扰动动能成数量级地放大,由下支解附近增长到局地波包的上支解,最终形成二维槽流的特征转捩结构[1]。

图2. 局地波包在不同雷诺数Re的衰减过程中(a) P和(b)D 随扰动动能Ek的变化。模拟所用初始扰动为在Rei所得的局地波包。Ek1和Ek2是Ek 衰减曲线上两个拐点处的扰动动能。(c) 公式(2)所得稳态解的Ek(Re)曲线(灰实线)同数值模拟的比较。[2]
Navier-Stokes(NS)方程线性算子的非正则性决定了扰动瞬态增长的存在,因此转捩特征结构的自维持性变得至关重要,决定着流动的非层流态是否会最终衰减回层流态。迄今为止,人们对特征转捩结构自维持性的判断仍是基于对实验或数值模拟结果的观测和统计分析。为了能从流体动力学角度理解亚临界转捩现象,课题组做了如下分析。首先,注意到局地波包的孤立特征和二维槽流的边界条件,可用由NS方程推得的Reynolds-Orr方程来严格地描述局地波包整体的扰动动能演化,
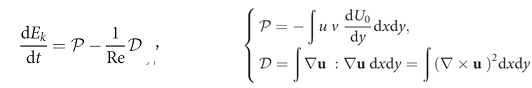 (1)
(1)
其中Ek是包含一个孤立波包的流场的扰动动能积分,P和D分别是扰动动能产生项和扰动拟涡能积分项,D/Re代表粘性耗散,(U0,0)为基本流流场。 其次,对孤立波包在低雷诺数时的衰减过程进行了数值模拟,发现其扰动强度在衰减过程中单调减小但形态基本不变,这强烈暗示孤立波包的P和D仅是扰动幅值或Ek的函数。为检验这一猜测,课题组以不同雷诺数Rei获得的具有不同扰动动能的波包作为初始扰动,在不同的低雷诺数下进行衰减过程的系统的大规模数值模拟。得到的Ek随时间的衰减曲线因Re和初始扰动动能(Rei)的不同而不同,然而如图2(a)(b)所示,所得的P和D曲线均重合在了一条曲线上。最后,基于波包衰减的数值模拟结果,提出了保形近似:波包的动能产生项P和拟涡能项D仅是扰动动能的函数,与雷诺数和初始扰动动能无关。波包的保形性质将多尺度结构给理论分析带来的困境大为缓解,可以容易地推得稳态时波包扰动动能应满足的关系式
P (Ek)/D (Ek) =Re, (2)
和转捩的阈值雷诺数Rec 表达式
Rec= P /D iff dD/dP =D/P. (3)
依据低雷诺数时衰减波包所得的P和D以及公式(2) 可预测在中高雷诺数发生转捩时稳态波包解的Ek曲线。如图2(c)中灰色实线所示,理论预测同数值模拟所得的上支解(UB)、下支解(LB)以及阈值雷诺数(Rec=2332)相一致。特别地,预测值不仅在阈值雷诺数附近同数值模拟结果相符,在很大的雷诺数范围内(如雷诺数可高至4000)下支解的预测值仍同模拟值很好地符合,再次确认了局地波包的保形性质。关于波包多尺度形态的选择机制此前已作分析[4],此处不再赘述。进一步地,在阈值雷诺数附近,将公式(1)在Ek衰减曲线的第一拐点处做泰勒展开,可将该动能方程转化为经典的描述鞍节点分岔的微分方程,从而解析地证明局地波包的上支解是稳定的从而是可自维持的稳态解。另外,数值模拟中还发现,当Re> 2500时最优扰动的动能正比于Re-3.8 [1];而在低雷诺数时波包的寿命同(Rec-Re)-1/2成正比,依据公式(1)和保形近似给出了这一标度律的理论解释[2]。
需要说明的是,尽管二维槽流同管流和三维槽流的亚临界转捩过程存在诸多相似之处,如都存在局地的特征转捩结构、这些结构在更高雷诺数时会发生分裂等,但二维槽流仍缺少三维转捩的一些重要特征,如扰动场的随机性,因此三维剪切流的亚临界转捩过程仍有待更深入的研究。
相关结果刚刚在Physics of Fluids作为featured Letter发表[1],第一作者为力学与工程科学系博士生张林森。该研究得到国家自然科学基金重大研究计划重点项目资助。
[1] L.S. Zhang, J.J. Tao (2023) Nonlinear optimal perturbations and formation mechanism of localized wave packet in channel flow, Phys. Fluids, 35, 051704.
[2] L.S. Zhang, J.J. Tao (2022) Pattern preservation during the decay and growth of localized wave packet in two-dimensional channel flow, Phys. Fluids, 34, 064110.
[3] S. Zammert and B. Eckhardt (2017) Harbingers and latecomers – the order of appearance of exact coherent structures in plane Poiseuille flow, J. Turbul., 18, 103–114.
[4] Y. Xiao, J.J. Tao, L.S. Zhang (2021) Self-sustaining and propagating mechanism of localized wave packet in plane-Poiseuille flow, Phys. Fluids, 33, 031706.










