博弈论是用来研究理性个体行为决策的有效方法，广泛应用于经济学、心理学、物理学、计算机科学和生物生态学等领域。针对经典博弈论中个体完全理性假设的局限性， Maynard Smith在1973年通过引入群体交互思想，把博弈理论分析和动态演化过程相结合，创立了演化博弈论这一新理论，为理解群体行为决策、信息传播动力学和群体智能涌现等重大科学问题提供了研究思路。

以往关于演化博弈论的研究，要么是基于确定性的个体适应度假设（即博弈交互中效用更高等同于策略传播范围更大），要么是基于Poisson过程的策略随机传播假设（即单位时间策略只随机传播到一个个体）。这些假设简化了理论分析过程，降低了研究难度，使得大量早期研究工作得以开展。但是，最近的实证研究表明，在群体交互和策略传播中普遍存在多种不确定性和随机性。也就是说，博弈交互中效用与策略传播范围不完全等同，策略的传播过程呈现出heavy-tailed分布特性，明显不同于Poisson过程。

图1：随机适应度的参数化模型以及样本轨道仿真

本论文摒弃了传统的确定性过程和Poisson过程模型，建立了一个通用的参数化随机适应度模型。在此模型中，收益越高的个体，适应度的期望会越高，同时其方差也会越大。在两策略博弈的情况下，系统的动力学过程可以近似为一个扩散过程，由一个二维随机微分方程所描述。系统的两个变量分别刻画了两种策略个体数目的变化。使用Ito公式对其进行坐标变换后，该系统可以用总个体数目和第一种策略的占比这两个变量描述。这个双变量系统是一个典型的快-慢系统，即系统在一个尺度上变化的速度远快于另一个尺度，可以对其进行尺度分离，将二维动力学简化为慢流形上的一个一维过程，最后通过求解Backward Kolmogorov方程得到固定概率，即演化动力学的方向。

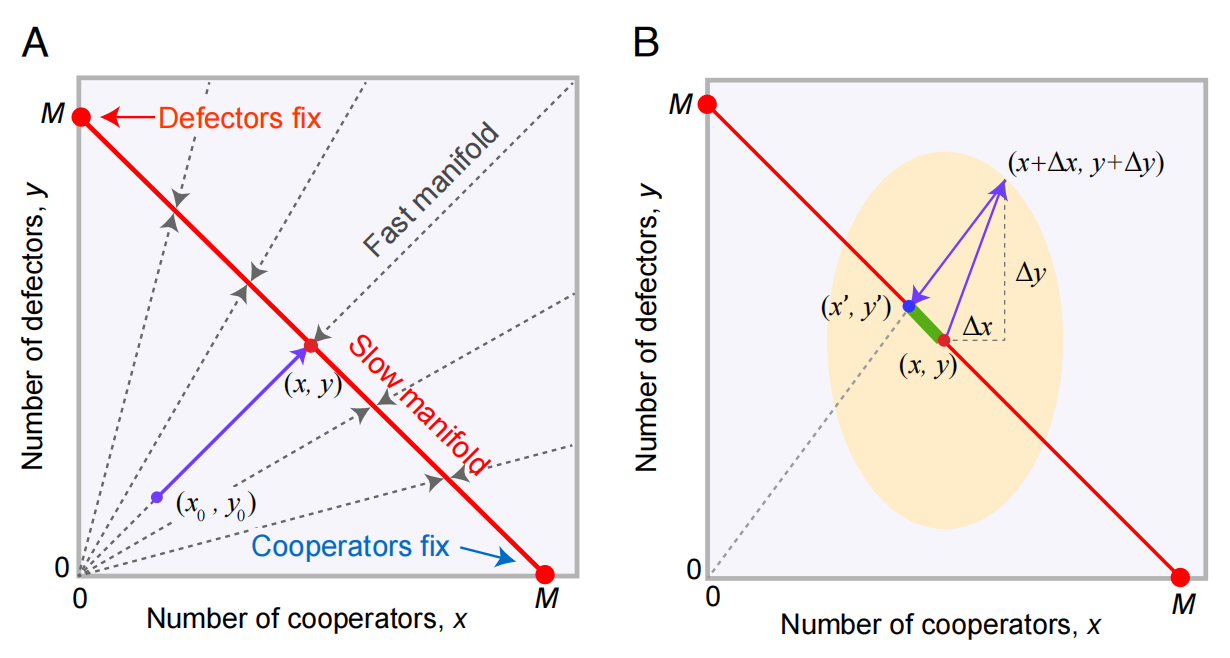
图2：快慢动力学的尺度分离

本文发现，相比于由常微分方程所描述的确定性系统，考虑了随机性的系统演化方向可能和确定性系统完全相反。例如，在经典的囚徒困境中，defector总是具有更高收益，复制动力学方程也表明系统总会朝着全是defector的方向演化。然而，在考虑了适应度的随机性之后，在一定条件时，系统演化的方向可以被逆转，朝着全是cooperator的方向演化。这一条件可以简单地表示为δ_2>M，其中δ_2描述个体之间方差的异质性程度，M表示系统达到准稳态时的个体数目。对于多策略博弈，该随机性也能改变系统的相图。比如对于Rock-Paper-Scissors博弈，随机性可以将原本稳定的焦点变为不稳定的焦点，并且逆转轨道旋转的方向。

该工作表明，随机性对于策略的动态演化是不可忽略的因素，甚至可以改变整个演化的方向。这对于解释群体行为的复杂性、合作涌现、群体决策与智能都具有重要意义。

本文第一作者为6163am银河线路2020级博士生王国丞，通讯作者为苏奇（6163am银河线路博士毕业生、美国宾夕法尼亚大学博士后）、王龙（6163am银河线路教授）、Joshua Plotkin（美国宾夕法尼亚大学教授）。

文章地址：https://www.pnas.org/doi/10.1073/pnas.2216218120